- Abrir el programa schematics.exe de
PSPICE. - Dibujar el circuito a simular, fijando las opciones
de configuración para la simulación y la manera que ha de aparecer
la exhibición en pantalla. En lugar del componente que
no se encuentra en las librerías se coloca otro con
características similares. - Guardar el archivo con
extensión .sch en el destino elegido.
- Seleccionar con el mouse y un
clic, el dispositivo del que se desean modificar sus
parámetros eléctricos. Para el ejemplo, se
seleccionó el SCR 2N1595, en un circuito como el que
aparece en la figura siguiente.
- En las opciones del menú principal ir a EDIT, y
dentro de ese menú, desplazarse hasta MODEL, como se
muestra en la
ilustración siguiente:
- Dar clic en MODEL, para que aparezca el cuadro de
dialogo EDIT
MODEL, como aparece en la figura de la página
contigua. - Dar clic en la opción EDIT INSTANCE MODEL, que
conducirá a un cuadro de dialogo MODEL EDITOR, en donde
se podrán modificar las características deseadas
SOLO PARA EL CIRCUITO EN CUESTIÓN. Lo único por
hacer es borrar el valor a modificar y anotar el que tiene el
dispositivo que nosotros usamos. Para finalizar dar clic en OK,
y simular.

PRÁCTICA 1:
MEDICIÓN DE LOS PARÁMETROS DEL
TIRISTOR
Un tiristor es un dispositivo semiconductor de
cuatro capas de estructura pnpn con tres uniones pn. Tiene
tres terminales: ánodo, cátodo y compuerta.
La figura 1.1 muestra el símbolo y el modelo
cristalino del tiristor.
Figura 1.1: Símbolo del
tiristor y tres uniones pn.Cuando el voltaje del ánodo se hace
positivo con respecto al cátodo, las uniones J1 y J3
tienen polarización directa o positiva. La
unión J2 tiene polarización inversa, y solo
fluirá una pequeña corriente de fuga llamada
corriente de estado inactivo ID. Se dice
entonces que el tiristor está en condición de
bloqueo directo en estado desactivado. Si el voltaje de
ánodo a cátodo VAK se incrementa a
un valor lo suficientemente grande, la unión J2
polarizada inversamente entrará en ruptura. Esto se
conoce como ruptura por avalancha y el voltaje
correspondiente se llama voltaje de ruptura directa
VB0. Dado que las uniones J1 y J3 tienen ya
polarización directa, habrá un movimiento libre de portadores a
través de las tres uniones, que provocará una
gran corriente directa del ánodo. Se dice entonces
que el dispositivo está en estado de
conducción o activado. La caída de voltaje se
deberá a la resistencia óhmica de las cuatro
capas y será pequeña, por lo común
cercana a 1 volt.La corriente del ánodo deberá ser
mayor que un valor conocido como corriente de enganche
IL, a fin de mantener la cantidad requerida de
flujo de portadores a través de la unión J2;
de lo contrario, al reducirse el voltaje del ánodo a
cátodo, el dispositivo regresará a la
condición de bloqueo. La corriente de enganche, es
la corriente de ánodo mínima requerida para
mantener el tiristor en estado de conducción
inmediatamente después de que ha sido activado y se
ha retirado la señal de la compuerta.Una vez que el tiristor está activado, se
comporta como un diodo en conducción y ya no hay
control sobre el dispositivo. El tiristor seguirá
conduciendo, porque en la unión J2 no existe una
capa de agotamiento debida a movimientos libres de
portadores. Sin embargo, si se reduce la corriente directa
del ánodo por debajo del nivel conocido como
corriente de mantenimiento IH, se genera una
región de agotamiento alrededor de la unión
J2 debida al número reducido de portadores; el
tiristor estará entonces en estado de bloqueo. La
corriente de mantenimiento es del orden de los miliamperios
y menor que la corriente de enganche. La corriente de
mantenimiento es la corriente de ánodo mínima
para mantener al tiristor en estado de régimen
permanente.Cuando el voltaje del cátodo es positivo
con respecto al ánodo, la unión J2 tiene
polarización directa, pero las uniones J1 y J3
tienen polarización inversa. Esto es similar a dos
diodos
conectados en serie con un voltaje inverso a través
de ellos. El tiristor estará en estado de bloqueo
inverso y una corriente de fuga, conocida como corriente de
fuga inversa IR fluirá a través
del dispositivo.Un tiristor se puede activar aumentado el voltaje
directo de ánodo a cátodo más
allá de VB0, pero esta forma de activarlo
puede ser destructiva. En la práctica, el voltaje
directo se mantiene por debajo de este valor, y el tiristor
se activa mediante la aplicación de un voltaje
positivo entre la compuerta y el cátodo.Lo anterior puede entenderse mejor cuando se
observa la gráfica de la curva característica
del tiristor, que se muestra en la figura 1.2.
Figura 1.2: Curva
característica del tiristor.- Marco teórico
1 SCR C106D
1 trimpot de 100K
1 resistencia de 2K ½ W
4 resistencias de 100k ½ W
1 resistencia de 47k ½ W
1 fuente de alimentación de 12
VCD1 micro amperímetro
1 interruptor (push)
- Material y equipo
En esta práctica se determinó el
valor real medido de las corrientes de enganche y de
mantenimiento en un tiristor comercial, así como el
valor de la corriente mínima de compuerta necesaria
para activar al dispositivo.1.3.1 Medición de la corriente
mínima de compuertaPara la medición de la corriente
mínima de compuerta, se utilizó el circuito
que se dibuja en la figura 1.3. Para el cálculo de los componentes se
tomó como referencia al manual
del fabricante, el cual proporciona los siguientes valores:Parámetro
Símbolo
Mín
Typ
Máx
Unidad
Corriente de disparo por
compuertaIGT
—
30
200
µA
Corriente de mantenimiento
IHX
0.3
—
3
mA
Corriente de conducción
(RMS)IT(RMS)
—
—
4
A
De acuerdo con la tabla anterior,
propusimos que por el tiristor circulara una corriente de
ánodo, por lo menos 10 veces mayor a la corriente de
mantenimiento, para que no tuviéramos problemas con el enganche y cebado del
tiristor. De esta forma, propusimos una corriente de
ánodo circulante por RL y T1 de 50mA. Lo que arroja
un valor de RL, correspondiente a los 12VCD que aplicamos,
de: ,por lo que aproximamos RL a 220
,por lo que aproximamos RL a 220
ohms.En cuanto a las R’s 2,3 y 4, y al trimpot
R1, consideramos que la corriente mínima es de
30µA, por lo que la resistencia de compuerta
máxima estaría dada teóricamente
por: ,lo
,lo
que justifica que este sea el valor serie de esos
elementos.El micro amperímetro µAmp, se conecta
en serie con la compuerta, y se desprecia la impedancia del
instrumento. µAmp2 servirá para detectar
cuando T1 este en estado de conducción.
Figura 1.3: Circuito para la
medición de la corriente de compuerta.Para poder
medir el valor real de la corriente de compuerta, se
ajustó el trimpot R1 a su máximo valor, se
encendió la fuente y se verificó que no
existiera flujo de corriente en µAmp2, en tanto en
µAmp fluían aproximadamente
30µA.Una vez hecho esto, R1 se disminuye lentamente de
valor hasta que el tiristor conduce (comprobándose
mediante µAmp2.) El valor de la corriente circulante
en la compuerta resultó ser de 35µA. La
resistencia medida en el arreglo serie fue de 330 kohms.
Para comprobar: ,lo
,lo
que concuerda con lo esperado.1.3.2 Medición de la corriente de
mantenimientoPara este propósito se ocupó el
circuito de la figura 1.4. Se utilizó una
resistencia de compuerta de 200k, que fija a la corriente
de compuerta en 60µA, que es mayor a
IGTmín y menor a
IGTmáx, lo que asegura el disparo por
compuerta.Para el cálculo de R1 (fija) y R2
(trimpot), que sumados son RL, se ocupó el siguiente
procedimiento: primero se supone que la corriente de
ánodo es igual a IH mínima dada
por el fabricante, por lo que:
En tanto que para IH máxima,
tenemos que el valor correspondiente de la resistencia de
carga es:
Todo esto significa que el valor de la resistencia
de carga deberá estar entre 4 y 40 kohms para
asegurarnos que la corriente de ánodo estará
dentro de los
valores esperados para la corriente de
mantenimiento.Para asegurar que la corriente de ánodo no
sea muy grande, por si acaso necesitamos reducir mucho el
valor del trimpot, aseguramos que R1 sea de 2 kohms, lo que
sugiere que R2 podrá variar libremente desde su
mínimo valor.
Figura 1.4: Circuito para medir la
corriente de mantenimientoPara medir la corriente de mantenimiento, se
fijó R2 a su mínimo valor, para asegurar que
la corriente anódica fuera mayor a la máxima
corriente de mantenimiento dada por el fabricante, y se
disparó el tiristor cerrando momentáneamente
el interruptor mostrado en la figura 1.4; se observó
que el tiristor cambió a conducción y se
mantuvo en ese estado. El valor de la corriente
anódica era de aproximadamente 6mA, como era de
esperarse, en tanto RL=2k.En estas condiciones, el tiristor estaba cebado.
Poco a poco se fue aumentando el valor de R2, en tanto la
corriente de ánodo se reducía por esta causa.
El tiristor dejó de conducir cuando la corriente en
µAmp era de aproximadamente 0.39mA; por lo tanto, la
corriente de mantenimiento del tiristor que estudiamos, es
ligeramente mayor a 0.39mA.1.3.3 Medición de la corriente de
enganche.A partir del circuito de la figura 1.4,
mantenemos el interruptor cerrado, y reducimos ligeramente
el valor del trimpot R2, abriendo de vez en cuando el
interruptor. El valor de la corriente de enganche es aquel
que, una vez que se ha abierto el interruptor, es decir,
que se retire el pulso de compuerta, el tiristor no regresa
al estado de bloqueo.El valor de la corriente de enganche que se obtuvo
mediante este procedimiento fue de 0.41mA. Esto indica que
la corriente de enganche es ligeramente menor a este
valor. - Desarrollo
- Conclusiones
Basándonos en los resultados obtenidos en esta
práctica, pudimos ver que los valores reales de los
parámetros del tiristor relacionados con su
activación, son muy cercanos a los valores mínimos
propuestos por el fabricante.
Para la corriente de compuesta, el fabricante propone un
valor mínimo de 30µA; en la práctica se
obtuvo un valor de 35µA para este parámetro. Para la
corriente de mantenimiento, se propone un valor mínimo de
0.3mA; obtuvimos 0.39mA para este parámetro. Para la
corriente de enganche, el fabricante no propone valor alguno,
pero se sabe que debe ser una poco mayor que la corriente de
mantenimiento; se obtuvo un valor de 0.41mA.
También fue posible reafirmar los conceptos de
corriente de compuerta, de mantenimiento y de
enganche.
Para la corriente de compuerta se sabe que es la
corriente, en el pulso de compuerta, necesaria para la
activación del tiristor. En efecto, comprobamos que si no
aplicábamos una corriente ligeramente mayor a 35µA,
el tiristor no encendía.
La corriente de mantenimiento es la corriente de
ánodo mínima para mantener al tiristor en estado de
régimen permanente en conducción. Se
comprobó que, una vez que el tiristor se disparaba, era
necesario mantener el flujo de corriente por arriba de 0.39mA
para mantener la conducción.
La corriente de enganche es la corriente de ánodo
mínima requerida para mantener el tiristor en estado de
conducción, inmediatamente después de que ha sido
activado y se ha retirado la señal de la compuerta.
Comprobamos que si no existían al menos 0.41mA, no era
posible que el tiristor se quedará cebado.
PRÁCTICA
2: CONMUTACIÓN FORZADA DEL SCR Y RED
SNUBBER
2.1 Marco teórico
2.1.1 Conmutación forzada
En algunos circuitos con tiristores, el voltaje de
entrada es de corriente directa. Como se sabe, el tiristor se
"amarra" en el estado de
conducción, en tanto es un dispositivo de enganche. Una
vez que el tiristor entra en conducción, es necesario que
su corriente anódica llegue a ser menor a la corriente de
mantenimiento.
Para poder controlar la conmutación del tiristor
en corriente directa existe una técnica llamada de
conmutación forzada, que consiste en agregar un circuito
adicional, cuya función es
obligar a que la corriente que fluye por el tiristor pase por
cero. Esta técnica encuentra aplicación en los
convertidores de dc a dc (pulsadores) y de dc a ac
(inversores.)
Hay una gran diversidad de circuitos de
conmutación forzada, entre los que podemos menciona al
circuito de auto conmutación, conmutación por
impulso, por pulso resonante, etc. En este caso trataremos de un
circuito de conmutación forzada basado en una red RC simple, y se
muestra en la figura 2.1.

Figura 2.1: Circuito para la
conmutación forzada
El circuito anterior opera de la siguiente manera:
Cuando se dispara el tiristor T1, la corriente de
conducción fluye a través de RL y por el
ánodo del tiristor, y si es mayor que la corriente de
mantenimiento, T1 quedará "cebado" cuando se haya retirado
el pulso de compuerta. Al mismo tiempo, el capacitor C se
cargará por medio de R, existiendo un potencial más
positivo en la terminal conectada al interruptor. Cuando cerramos
el interruptor, el capacitor se descargará sobre el
tiristor, polarizándolo inversamente; de esta forma, el
voltaje en el tiristor adquiere un potencial inverso, obligando a
la corriente que fluye por él a intentar cambiar de
dirección, lo que la obligará a
pasar por cero.
Adicionalmente se debe decir que es necesario que el
tiempo de carga del capacitor sea menor a la frecuencia de la
señal de activación de la compuerta, y al mismo
tiempo, mayor que el tiempo de apagado del tiristor T1, para que
el circuito de conmutación no influya en el funcionamiento
principal del circuito.
El circuito tiene una limitación: solo se
garantiza su funcionamiento para cargas resistivas, ya que en
presencia de cargas inductivas sería necesario considerar
el efecto del desfasamiento de la corriente provocado por la
carga.
2.1.2 Red Snubber
La red Snubber es un arreglo RC que se conecta en
paralelo al tiristor en un circuito de conmutación, como
una protección para el dv/dt. Es básicamente un
circuito de frenado al apagado del tiristor, cuyo objetivo es
amortiguar el efecto de una variación voltaje / tiempo que
en algún momento pudiera ser destructiva para el
tiristor.
El diagrama del circuito correspondiente a la red
Snubber se muestra en la figura 2.2. La relación de sus
componentes está dada por:
![]()
Es importante saber que el valor de la resistencia Rs,
está ligado a la corriente de descarga, ITD
(que circulará cuando se descargue el capacitor), y que
siempre se sugiere unas 10 veces mayor a la corriente de la
carga. De esta forma:
![]()
Por consiguiente, si se conoce el valor de la carga R, y
se sugiere el valor de la corriente de descarga, puede
encontrarse fácilmente el capacitor a usar.

Figura 2.2: Tiristor con red
Snubber
2.2 Material y equipo
1 SCR C106D
1 capacitor de 100µf 50V
1 capacitor de 1000µ 50V
1 foco de 12V para DC 3W
1 resistencia de 47 ohms ½ W
1 resistencia de 15 ohms ½ W
1 fuente de alimentación de 12VDC
2 interruptores (push)
2.3 Desarrollo
En esta práctica se demostró que mediante
el circuito de conmutación forzada es posible hacer pasar
al tiristor de su estado de conducción al de bloqueo,
cuando está funcionando en corriente directa.
Fue posible también implementar la red Snubber
para la protección en el apagado, comprobándose que
no había efectos visibles de su utilización sobre
el funcionamiento del circuito de conmutación
forzada.
2.3.1 Implementación del circuito de
conmutación forzada
El circuito de conmutación forzada se armó
con base en el circuito de la figura 2.1. Los valores de R y C se
calcularon mediante la constante de tiempo, suponiendo que este
es el tiempo de carga y descarga del capacitor. Obviamente esto
es solo una aproximación empírica.
Se realizaron dos pruebas: en la
primera (figura 2.2) se usó un capacitor de 100µF, y
se supuso una constante de tiempo de 5ms. Por esta razón R
se calculó como R=T/C=4ms/100µF=40 ohms. Se
aproximó a 47 ohms.
Para la segunda prueba se utilizó la misma
resistencia R de 47 ohms, y se sustituyó el capacitor por
uno de 1000µf.
Para comprobar el funcionamiento del circuito de la
figura 2.3, se realizó lo siguiente:
Una vez encendida la fuente de alimentación, se
aplicó el pulso de compuerta mediante PB1 (la
representación del diagrama no corresponde a este tipo de
interruptor, pero considérese como tal), de tal forma que
el tiristor se encendía y se mantenía en
conducción, y la lámpara L1 encendía. Una
vez hecho esto, se oprimía PB2 y la lámpara se
apagaba, debido a la descarga de la carga del capacitor sobre el
tiristor.
Debe comentarse que no se notó variación a
simple vista cuando se sustituyó a C de 100µF a
1000µF.

Figura 2.3: Circuito para montaje
práctico
Nota: la resistencia de compuerta del circuito se
usó, según la práctica anterior, con una
valor de 200k. La resistencia RL representa a la lámpara y
su valor se calculó mediante RL=V*V/P=12*12/3=48
ohms.
2.3.1.1 Simulación del circuito de
conmutación forzada
Para entender el comportamiento
real del circuito de conmutación forzada, simulamos el
circuito que se dibuja en la figura 2.4. En este circuito se
colocó a PB1 como un interruptor formado por un
interruptor comúnmente abierto y uno comúnmente
cerrado, para simular que es un interruptor de pulso
(push.)

Figura 2.4: Circuito de
conmutación forzada para simular
En la figura 2.5 se dibuja una gráfica del
voltaje en la carga y en el tiristor, en donde se aprecia que,
una vez que se enciende el tiristor, existe en la carga un
voltaje cercano a los 12 V de alimentación, y cuando se
cierra el interruptor PB2, el voltaje en la carga decrece hasta
cero.
Puede notarse también que la carga se polariza
con un voltaje aproximado del doble del valor de la fuente, en
tanto en el tiristor se presenta un voltaje inverso de 12 V. Lo
anterior es debido a la descarga del capacitor, por lo que debe
considerarse esta característica del circuito en el
diseño
de las características de los componentes, ya que es un
transitorio de magnitud importante.
En la figura 2.6 se observan las formas de onda de la
simulación del circuito para un valor del capacitor de
1000 µF, y se aprecia que no existe un cambio
sustantivo en las formas de onda, a no ser porque el voltaje de
descarga del capacitor desciende más
lentamente.

Figura 2.5: Formas de onda del circuito
de conmutación forzada para C=100 µF
Es importante hacer notar que, para la simulación
del circuito, las librerías de PSPICE 6.0, no contienen al
SCR C106D, que se usó en la práctica, por lo que se
recurrió al procedimiento mostrado en CONSIDERACIONES
GENERALES, para modificar el modelo original del SCR
2N1595.

Figura 2.6: Formas de onda del circuito
de conmutación forzada para C=1000 µF
2.3.2 Implementación del circuito adicionando
la red Snubber
Para el diseño de la red Snubber, primero
se calculó el valor de la resistencia en serie
RS, sin embargo, para que el cálculo de la
misma fuera idéntico para todas las prácticas de
este manual, se consideró que la carga a utilizar era un
foco de 100 W, para 130 VAC; de esta forma, la resistencia
equivalente de la carga es:
![]() , que
, que
para simplificar se utilizará de 160 ohms.
A partir del resultado anterior, se puede determinar que
la corriente nominal de la carga es de:
![]()
De esta forma, si consideramos que la corriente de
descarga es 10 veces la corriente nominal, tenemos
que:
![]() , por lo
, por lo
que se utilizará un valor de 15 ohms
Para el cálculo del capacitor CS, con
todas las consideraciones anteriores, se tiene que:
![]() , que se
, que se
llevará a 68 nF
2.3.2.1 Simulación del circuito
El circuito práctico para simular el circuito de
conmutación forzada con red Snubber se dibuja en la figura
2.7.

Figura 2.7: Circuito con red
Snubber
La figura 2.8 contiene las gráficas de las formas de onda del
circuito, en donde se puede observar el voltaje entre
ánodo y cátodo del tiristor, el voltaje en el
capacitor Cs, y la corriente en la resistencia Rs.
Puede notarse en dicha figura que el comportamiento del
circuito no se altera. Así mismo se observa que el voltaje
en el capacitor CS es igual al voltaje en el tiristor,
y que la corriente en Rs es cero, excepto en los instantes de
conmutación.
La red Snubber provoca también una
disminución en los transitorios provocados al momento del
apagado por la descarga del capacitor, lo que protege
visiblemente al tiristor. Precisamente la red es del tipo "freno
al apagado".

Figura 2.8: Formas de onda del circuito
con freno al apagado
2.4 Conclusiones
Como conclusiones generales acerca del circuito de
conmutación forzada, podemos decir que es un circuito para
provocar la conmutación del SCR cuando este opera en
corriente directa.
Debe mencionarse que este circuito no es apto para
conmutar a velocidades grandes, ya a que el tiempo de apagado es
relativamente grande, debido al tiempo de carga y descarga del
capacitor.
Conviene decir también que la operación de
la conmutación forzada implica la inserción de un
transitorio considerable a la carga y al tiristor.
En cuanto a la red Snubber, es un circuito de
protección, por lo que no afecta sustantivamente el
funcionamiento del circuito al que se agrega. La
protección que aporta consiste en un freno a las
pendientes pronunciadas de tensión al momento del apagado
del dispositivo.
3.1 Marco teórico
Unas cuantas aplicaciones del SCR se basan en el control
de la corriente de compuerta por medio del control de una
resistencia limitadora. Como ejemplos sencillos de tales
aplicaciones tenemos al control manual de la intensidad de
iluminación en lámparas o focos, como los usados en
las lámparas de buró en las habitaciones de las
casas, o en las lámparas de los cines y teatros, en los
cuales se necesita la variación gradual de la cantidad de
luz, para
lograr un ambiente
adecuado al lugar.
Un circuito con la estructura que se aprecia en la
figura 3.1 es capaz de controlar el ángulo de disparo del
SCR entre 0 y 90 grados eléctricos. El control del
ángulo de disparo implica determinar en qué momento
se activará el SCR para un ciclo de la señal de
entrada, o sea, se modificará la porción de tiempo
que conducirá el dispositivo, con relación a la
señal de alimentación de voltaje.

Figura 3.1: Circuito para disparo
resistivo
En el circuito de la figura 3.1, la variación del
ángulo de disparo se logra mediante la variación de
la resistencia R1, que es la resistencia limitadora de la
corriente de compuerta, y R2 es la carga, o sea una
lámpara o foco, para los ejemplos que se han
citado.
3.2 Material y equipo
1 SCR C106D
1 capacitor de 0.1µ 250V
1 resistencia de 15 ohms ½ W
1 foco de 120V 100W
1 potenciómetro de 1Mohms
1 potenciómetro de 4.7Mohms
1 transformador de aislamiento 1:1
1 fusible 2A 250V
3.3 Diseño del circuito
Para el diseño del circuito se tomaron
como punto de partida las consideraciones siguientes:
Se necesita diseñar un control de disparo
resistivo que permita la manipulación del ángulo de
disparo del SCR C106D entre 10º y 80º, teniendo una
fuente de alimentación de 180 Vp a 60Hz. La carga
será un foco de 100W, cuya resistencia de carga
equivalente ya se ha calculado en una práctica anterior
como 160 ohms.
Con aquellas consideraciones, el siguiente paso es
encontrar las características del SCR que usaremos, siendo
la que nos interesa, la IGT, que se ha convenido usar
como 35µA, según los resultados de la
práctica 1.
Con todo lo anterior, si se propone el circuito de la
figura 3.2 como el circuito práctico a usar, donde RL es
el foco de 100W (160ohms), R1 es la resistencia limitadora de
compuerta para el disparo al ángulo mínimo
(10º) y R2 es un potenciómetro que controlará
a partir de 10º y hasta 80º, el cálculo de los
componentes mencionados está dado por:
![]()
Dado que este valor no es comercial, se colocará
un potenciómetro de 1Mohm, ajustado aproximadamente a este
valor.
![]()
De este modo, R2 será un potenciómetro de
4.7Momhs, que será el que deberá moverse para
lograra el rango de ángulo de disparo deseado.
3.4 Simulación del circuito
Para verificar el comportamiento del circuito, se
simuló en PSPICE 6.0, modificando las
características eléctricas del tiristor, mediante
el procedimiento descrito en CONSIDERACIONES GENERALES, para que
se ajustara a las características del SCR C106D, que se
usó en la práctica.
La figura 3.2 muestra el circuito que se usó para
la simulación, y el mismo que se usó en la
práctica. En la práctica se agregó el
transformador de aislamiento y el fusible, así como la red
Snnuber para el tiristor.

Figura 3.2: Diagrama del circuito de
disparo resistivo
Para comprobar los resultados de la simulación
con lo esperado teóricamente, el circuito se simuló
en los casos extremos, cuando R2 tiene un valor cero, es decir,
la resistencia limitadora de compuerta vale 892k (disparo a
10º), y cuando R2 tiene un valor de 4.17M (disparo a
80º.)
En la gráfica de la figura 3.3 se muestra la
simulación para un valor de R1 de 892k y R2 de 1ohm, de
tal forma que no se tome en cuenta, y sea como si solo estuviera
la resistencia ajustada a 892k para que el disparo ocurra a
10º.

Figura 3.3: Disparo a
10º.
Como puede apreciarse, el disparo ocurrió a
580µs aproximadamente, lo que representa un disparo real en
grados de:
![]()
Para la figura 3.4, que es la simulación cuando
R2 tiene un valor de 4.17Mohms, se espera un disparo a
80º.

Figura 3.4: Disparo a
80º.
Se ve claramente en la figura anterior que el disparo
real ocurrió a los 3.63ms, que coincide con un
ángulo en grados de:
![]()
Ambos valores para el ángulo de disparo difieren
solo por 2º, aproximadamente, de lo que se esperaba
idealmente.
3.5 Resultados prácticos y
conclusiones
Cuando se implementó el circuito en la
práctica, los resultados obtenidos fueron muy aproximados
a lo esperado teóricamente, ya que, para el valor de R2
mínimo se obtuvo un ángulo de disparo (visto en el
osciloscopio),
de unos 14º, y para el valor máximo de la misma
resistencia, se logró un valor cercano a los
82º.
Cabe mencionar que, debido a que R2 tenía un
alcance aún mayor de lo requerido (4.7M, cuando se
necesitaban 4.17M), el valor del ángulo de disparo pudo
ser de casi 90º.
El efecto visual logrado en el foco fue el siguiente:
cuando se colocaba el potenciómetro R2 en su valor
máximo, el foco apenas se encendía, pero a medida
que se giraba hacia su mínimo valor, se incrementaba la
intensidad de la luz que emitía, lográndose la
máximo intensidad cuando R2 era prácticamente
cero.
4.1 Marco teórico
El valor de la corriente de corriente de compuerta de
los tiristores suele variar demasiado, aún en los
tiristores de la misma matrícula. Esto se debe a que la
estructura de los cristales de material semiconductor nunca puede
ser idéntica de un dispositivo a otro. La diferencia entre
las características eléctricas de la compuerta de
los tiristores es aún mayor cuando los dispositivos
manejan grandes corrientes y voltajes.
Lo anterior implicaría que cada que se reemplace
un tiristor en un circuito, se tendría que diseñar
nuevamente la red resistiva, lo que vuelve impráctico un
circuito como el analizado en la práctica
anterior.
La forma más simple de solucionar el problema
planteado es colocar una red de adelanto RC para lograr un
disparo por voltaje y no por corriente. Para demostrar lo
mencionado refiérase a la figura 4.1.

Figura 4.1: Red RC de primer
orden
La función de transferencia del circuito, en el
dominio de la
frecuencia está dada por:
![]()
En donde el desplazamiento de fase del circuito y la
tensión de salida en función de dicho
desplazamiento se pueden simplificar en las
expresiones:
![]() , como el
, como el
ángulo de desplazamiento y
![]() , como el
, como el
valor de la tensión de disparo.
Como puede notarse, en ninguna de las expresiones se
incluye la corriente de compuerta, que si se supone de un valor
tan pequeño como para superarse a cualquier valor de Vgt,
el circuito constituye una red de disparo del tiristor por
voltaje.
Según las expresiones anteriores, se han
diseñado redes típicas de
disparo por control de fase, en donde el elemento de control es
el valor de R, que son capaces de disparar SCR’s y
TRIAC’s en ángulos de disparo que van de los
10º hasta casi 90º para redes de primer
orden.
De esta forma, debido a que se pueden colocar redes en
cascada para lograr ángulos de adelanto hasta de 180ª
(una red de segundo orden), entonces es posible superar el
ángulo de disparo, y en ocasiones, pueden alcanzarse
ángulos de disparo de unos 170º o
más.
Debe recordarse que no es posible alcanzar un
ángulo de disparo, ni a partir de cero, ni hasta
180º, debido a que la red RC tiene ganancia unitaria solo a
determinado valor de resistencia.
4.2 Material y Equipo
1 SCR C106D
3 capacitores de
0.1µ 250V
1 resistencia de 15 ohms ½ W
1 foco de 120V 100W
1 potenciómetro de 1Mohms
2 resistencias de 4.7k
1 potenciómetro de 4.7Mohms
1 transformador de aislamiento 1:1
1 fusible 2A 250V
4.3 Montaje de la red de disparo por
voltaje
4.3.1 Red de primer orden
Como se ha mencionado, el diseño de la red RC no
se efectúa directamente de las ecuaciones ya
que, en especial la última (Vgt), es solo una
aproximación en la que se desprecian los valores de la
corriente de compuerta, así como las capacitancias
internas de la compuertas o los efectos de la temperatura sobre
estos dos valores, principalmente.
Por lo anterior, se han diseñado redes que
responden adecuadamente a la frecuencia de la línea de CFE
y a valores de fase más o menos consistentes para las
variaciones de los parámetros del tiristor.
Con lo anterior, se usará la red de adelanto
típica que se analizó en clase, que corresponde al
circuito de disparo de la figura 4.2, en donde se proponen
valores para R desde 4.7k hasta poco más de 1M, y C ha
sido definido con un valor de 0.1µF.
Existe, según el mismo circuito de la figura 4.2,
un solo valor que se desconoce para el montaje del circuito: la
resistencia de carga. Sin embargo, en prácticas anteriores
se ha comentado que se usará un valor de 160 ohms para la
resistencia equivalente de la lámpara incandescente de
100W.
Bajo las condiciones descritas, puede calcularse el
ángulo de disparo mínimo y máximo, mediante
las ecuaciones siguientes:
![]() y
y
![]()
Por lo que para los valores propuestos en la figura 4.2,
la fase de adelanto (y el ángulo de disparo) está
dado por:
![]()
![]()
En la práctica estos valores se mejoraron
mediante el ajuste de la resistencia de límite R1,
alcanzando ángulos de disparo de hasta
90º.

Figura 4.2: Red de disparo RC de primer
orden
4.3.2 Red de disparo de segundo orden
La colocación en cascada de dos redes de primer
orden, como se indica en la figura 4.3 da lugar a una red RC de
adelanto de segundo orden. Esta red es capaz de proporcionar un
ángulo de disparo desde casi cero hasta casi 180º. El
principio de funcionamiento es el mismo que para una red de
primer orden, pero el desfasamiento de la tensión Vgt es
mucho mayor.
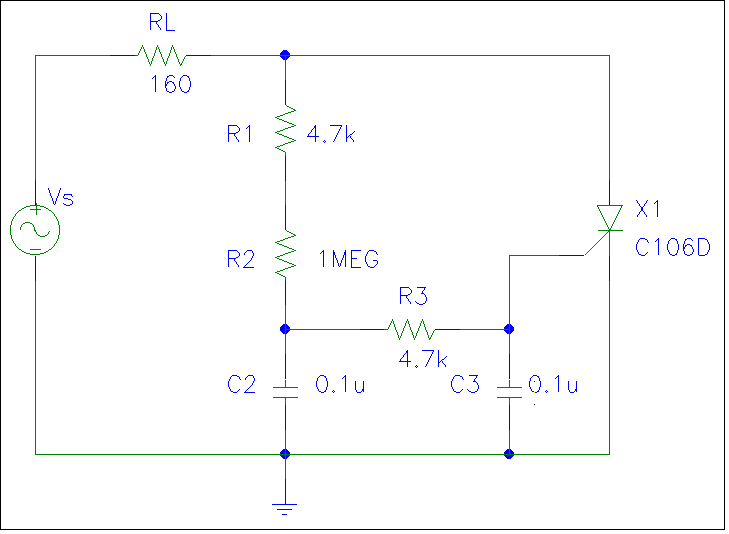
Figura 4.3: Red RC de segundo
orden
4.4 Simulación de los circuitos
RC
4.4.1 Red de primer orden
El circuito usado para la simulación se muestra
en la figura 4.4. Debe recordarse que han sido modificados los
parámetros del SCR de tal manera que estén dentro
del rango del SCR usado (C106D); así mismo, se incluye la
red Snubber, que ha sido diseñada previamente.

Figura 4.4: Circuito para
simulación de la red RC de primer orden
De acuerdo al circuito anterior, cuando R2 se encuentra
en su mínimo valor (supuesto de 1 ohm en la
simulación), se genera la señal de la figura 4.5 en
la carga. Puede apreciarse que el tiempo de retraso en el disparo
es de 515µs aproximadamente, que corresponde a un
ángulo de disparo de 11.12º, cuando se esperaba de
poco más de 10º.
Cabe mencionar que la medición en la
gráfica se tomó en el segundo ciclo, puesto que el
primero no es adecuado debido al proceso de
aproximación de PSPICE.

Figura 4.5: Forma de la señal en
la carga para el ángulo mínimo
De una forma similar, la figura 4.6 contiene la forma de
onda de la señal en la carga cuando R2 se encuentra en su
máximo valor (1Mohms).
Se puede apreciar que el cursor señala un tiempo
de retardo en el disparo de unos 3.832ms, que corresponden a
83º aproximadamente, que se acercan a los 88º deseados,
según los cálculos.
Se recuerda, sin embargo, que en la práctica,
mediante el ajuste de la resistencia R1, se logró mejorar
el valor del ángulo máximo de disparo, alcanzando
los 90º.
Nuevamente, en la gráfica 4.6 se aprecia que el
primer ciclo de la señal no es lo esperado, pero se ve que
en los siguientes ciclos, la señal se
establece.

Figura 4.6: Forma de onda en la carga
para el ángulo máximo.
4.4.2 Red de segundo orden
Para la simulación de la red de segundo orden, se
usó el circuito de la figura 4.7.

Figura 4.7: Circuito para la
simulación de la red RC de segundo orden

Figura 4.8: Forma de onda para red de
segundo orden, valor mínimo del ángulo

Figura 4.9: Forma de onda para red de
segundo orden, valor máximo del ángulo
Puede apreciarse como mediante la manipulación de
una sola resistencia (R2), se logró hacer varía el
ángulo de disparo desde 25º hasta 125º, como
puede verse en las figuras 4.8 y 4.9, que si bien no son los
valores que la teoría
propone (10º para el valor mínimo, casi 180º
para el máximo), son muestra de la mejora que se tiene
sobre el control del ángulo de disparo. Además, los
resultados prácticos resultaron ser mejores, debido a que
se pudo variar directamente el valor de R1 y R3, para incrementar
aún más la selectividad del
ángulo.
4.5 Conclusiones
Una red RC de adelanto permite disparar un tiristor por
voltaje y no por corriente, en tanto se suponga que su Igt es muy
pequeña, permitiendo así un mejor control del
ángulo de disparo, independiente del valor de
Igt.
La red básica de adelanto, de primer orden,
permite ángulos de disparo entre 10 y 90º, en tanto
la red de segundo orden puede extenderse hasta aproximarse
bastante a los 180º.
Las ecuaciones teóricas para el ángulo y
voltaje de disparo son aproximaciones, ya que no toman en cuenta
las variaciones de las características de los tiristores;
sin embargo, se han propuesto redes RC "prediseñadas" para
usar la frecuencia y voltaje de la línea de CFE. Estas
redes son además ajustables, puesto que permiten que se
adecue el ángulo de disparo mediante la variación
de una o dos resistencias, y no implica el rediseño de la
red, como en el caso del disparo resistivo.
5.1 Marco Teórico
Los circuitos de disparo analizados en las
prácticas anteriores utilizan el control de fase de una
señal sinusoidal aplicada a la compuerta del tiristor, lo
que implica una disipación constante de potencia en la
unión de compuerta del tiristor.
La utilización de un elemento de
conmutación como el DIAC, en conjunto con la red RC de
control de fase vista anteriormente forman un circuito capaz de
generar un impulso de disparo en lugar de una señal
sinusoidal. Con esta premisa, se sabe que el tiristor no
desperdiciará potencia en su compuerta.
Ahora bien, suponiendo que no se usara un DIAC para el
disparo de un TRIAC, sino solo la red RC, existiría
entonces un inconveniente: la constante de adelanto de la red
implicaría la existencia de una corriente remanente
inversa al ciclo de conducción. Es decir, al ser el TRIAC
un dispositivo que se activa en ambas polarizaciones, cuando la
señal de entrada cambiara de signo, el TRIAC
tendería a activarse con una corriente de sentido opuesto
al adecuado en su compuerta, debido al desfasamiento corriente
– voltaje que genera la red RC, lo que implicaría un
control sumamente preciso del desfasamiento que provoca la red RC
para evitar dicho fenómeno.
Existe aún otra ventaja importante de este
circuito sobre los que se vieron con anterioridad: el DIAC, por
ser un dispositivo de disparo por voltaje, siempre se
activará a la misma tensión (su voltaje de
ruptura), permitiendo así un mejor control del
ángulo de disparo del pulso aplicado a la compuerta del
tiristor.
5.2 Material y Equipo
1 TRIAC BTA08004
1 DIAC DB3 (30V)
3 capacitores de 0.1µ 250V
1 resistencia de 15 ohms ½ W
1 foco de 120V 100W
1 potenciómetro de 1Mohms
1 resistencias de 4.7k
1 transformador de aislamiento 1:1
1 fusible 2A 250V
5.3 Montaje del circuito
Como se ha mencionado, puede usarse la red RC que se
propuso en la práctica 4, y un DIAC, para formar un
circuito como el que se aprecia en la figura 5.1, que constituye
un circuito típico de disparo con DIAC.

Figura 5.1: Circuito de disparo con
DIAC.
El funcionamiento del circuito es como se indica: En el
primer semiciclo de la tensión de entrada Vs, el
condensador C1 se cargará mediante la resistencia en serie
formada por R2, RL y R1.
X2 es un DIAC de 30V de voltaje de ruptura, por lo que
cuando la tensión en la red RC alcance este valor, el DIAC
comenzará su conducción, permitiendo que el
condensador descargue un pulso de voltaje y corriente sobre la
compuerta del TRIAC X1, disparándolo. El pulso
durará hasta que finalice el semiciclo.
Durante el siguiente semiciclo, las polaridades de
corriente en voltaje se invierten, pero el principio de
operación es el mismo, puesto que ambos, TRIAC y DIAC son
dispositivos bidireccionales.
En la figura se muestra el circuito incluyendo la red
Snubber diseñada previamente, que también puede
usarse con TRIAC’s.
En la práctica, se lograron ángulos de
disparo de poco menos de 10º hasta casi 180º. Esto es
posible debido a que el condensador se carga prácticamente
desde un valor de tensión cero hasta el voltaje de
línea, existiendo solo una porción en el comienzo
de cada semiciclo en donde el condensador no tendrá carga
suficiente para activar al TRIAC.
El circuito no pudo ser simulado, debido a que en las
librerías de PSPICE no se encontró un DIAC,
necesario para simular el efecto deseado.
PRÁCTICA
6: DISPARO CON OSCILADOR DE RELAJACIÓN
6.1. Marco teórico
El transistor
monounión (UJT) se utiliza comúnmente para generar
señales de disparo en los SCR, mediante un circuito
conocido como oscilador de relajación, el cual se muestra
en la figura 6.1.

Figura 6.1: Diagrama básico del
oscilador de relajación.
El oscilador de relajación genera impulsos de
disparo cuya forma de onda del voltaje el RB1 es
idéntica a la forma de onda de la corriente de descarga
del capacitor CE; este voltaje debe diseñarse
tan grande como para activar al SCR.
El periodo de oscilación de la señal de
salida controlarse a partir de la variación de la
constante de tiempo formada por RE y CE.
Estos circuitos se diseñan para un propósito
específico, y las expresiones usadas en el diseño
que aquí se presenta están basadas en
consideraciones teórico –
prácticas.
6.2. Diseño del oscilador de
relajación
Para el diseño del circuito que se muestra en la
figura 6.2, se tomaron en consideración los siguientes
datos de
partida:
- La fuente de corriente alterna tiene un valor de 180
Vpp, a 60 Hz. - El voltaje de polarización del oscilador de
relajación es de 20 Vdc. - El valor de la carga, puramente resistiva, tanto para
las pruebas en corriente alterna como en directa, se
consideró con un valor dado por:
![]() ohms.
ohms.

Figura 6.2: Diagrama del circuito de
disparo con UJT
El fabricante del UJT proporciona los siguientes valores
para los parámetros principales del dispositivo, cuando se
supone que el voltaje interbases (VBB) es igual al
voltaje de alimentación del oscilador, es decir 20
V.
- La relación intrínseca
(h ) es de
0.7 - Corriente de pico (IP) de 1
µA - Corriente de valle (IV) de 4.5
mA - Voltaje de valle (VV) de 1.66
V - Resistencia interbases (RBB) de 6.9
kohms - Voltaje VF de 0.49 V @ 25º
C - Voltaje de pico de 14.49 V
El último punto a considerar para el
diseño es que se desea controlar el ángulo de
disparo del SCR de 10º a 170º eléctricos. Por lo
tanto, el rango de frecuencia de oscilación estará
dado por:
![]() ,
,
Donde a es el
ángulo de disparo y T es el periodo de la señal
alterna.
![]()
![]()
De acuerdo a lo anterior, la frecuencia de
oscilación del circuito tendrá que estar dentro del
rango de 127 a 2160 Hz.
A partir de todos los datos anteriores, es posible
calcular el rango de la resistencia de emisor válido para
el circuito:
![]()
![]()
![]()
Lo anterior implica que la resistencia de emisor debe
estar en un rango que va desde los 4K, hasta los 5.5M, y el mejor
valor es 40K. Sustituyendo este valor en la expresión que
relaciona a la frecuencia de oscilación con los elementos
del circuito, tenemos:

De esta forma, se eligió un valor comercial de
0.01 µF para el capacitor de emisor, y a partir de dicho
valor se recalculó RE para la frecuencia
máxima:

Este valor se adaptó a una resistencia comercial
de 33 K, para asegurar que se controlará la
oscilación desde los 10º. El valor de RE
para la frecuencia mínima estará dado
por:
 3
3
Para controlar fácilmente el rango de
variación de RE, se colocó un arreglo
serie de una resistencia de 33 K y un potenciómetro de 1
M, para asegurar la cobertura del control del ángulo de
disparo. De esta forma, en la figura 2 se tiene:
![]()
Los valores de R1 y R2 se obtuvieron mediante las
expresiones empíricas, y están dados
por:
![]() y
y ![]()
6.3. Simulación del circuito
El circuito de la figura 6.2 se simuló en dos
partes: primero se realizaron las pruebas con la carga en
corriente alterna, y después con la carga en corriente
directa. Además, para cada parte, se simuló el
disparo para 10º y para 170º.
En ambas simulaciones, el voltaje Vcc del oscilador se
obtuvo a partir de la conexión en serie de dos diodos
zener de 10 V cada uno, diodos cuya corriente se limita por la
resistencia en serie Rs. Los diodos rectificadores tienen
matrícula 1N4007.
6.3.1 Carga en el lado de alterna
Para simular el efecto del circuito sobre la
carga en el lado de alterna, se tomó el circuito que se
dibuja en la figura 6.2.
Primero se colocó RE2 de 1 ohm, para
suponer que solo estaba presente el efecto de RE1, de
tal manera que la resistencia de emisor tendría un valor
de 33 K aproximadamente. Es decir, el oscilador de
relajación estaría funcionando a su frecuencia
máxima, y por lo tanto, el SCR se tiene que disparar a
10º.
En la figura 6.3 se muestra la gráfica obtenida
en la simulación, para la señal en la carga y la
señal de disparo en la compuerta del tiristor.

Figura 6.3. Efecto en la carga de alterna
(10º)
Como puede verse en la figura 6.3, la señal en la
carga indica que el circuito se ha disparado (comienza un voltaje
en la carga RL), cuando se aplica el pulso en la compuerta
(VGx1), que a su vez proviene del oscilador de
relajación.
La posición del cursor para V(RL:1,RL:2), indica
que la conducción hacia la carga comienza en 573.9614
µs, lo que sugiere un ángulo de disparo de
12.44º, que se aproxima mucho al valor de 10º esperado
para los 33 K en la resistencia de emisor.
En la figura 6.4 se aprecian las dimensiones del pulso
de disparo en la compuerta, que presenta una amplitud aproximada
de 4.7 V y un ancho de pulso de 2.36 µs; esto demuestra que
el pulso generado es capaz de disparar al SCR.

Figura 6.4: Dimensiones del impulso de
disparo
En la figura 6.5 puede verse que, cuando comienza la
conducción, el voltaje de polarización del
oscilador de relajación cae a un valor muy bajo, lo que
provoca que el oscilador deje de funcionar, motivo por el cual no
se provocan impulsos luego del disparo ni antes de que termine el
ciclo de la señal de entrada. Lo anterior es debido a que
el SCR se amarra, y como el oscilador se alimenta del voltaje de
ánodo, se sabe que en conducción, este voltaje es
cercano a 1 V.
Puede notarse también que el voltaje de
alimentación no supera los 20 V, lo cual se debe al diodo
zener que regula el voltaje hacia el circuito.
La figura 6.6 está ilustrando el efecto del
disparo cuando RE tiene un valor de 655 K, lo que
quiere decir que si RE1 tiene un valor de 33 K, el
potenciómetro RE2 tendrá que ajustarse a
622 K para lograr el valor indicado de la resistencia de emisor,
que como se dijo anteriormente es la suma de RE1 y
RE2.

Figura 6.5: Efecto en la
alimentación del oscilador

Figura 6.6. Efecto en la carga de alterna
(170º)
Como puede verse en la gráfica anterior, el
disparo del circuito ocurre en 6.2768 ms, lo que significa que se
tiene un ángulo de conducción de 136º
aproximadamente. Al valor elegido de RE, se supone que el valor
del ángulo de conducción debía ser
170º; sin embargo, debido a que en esta zona la
polarización del oscilador comienza a decrecer debido a
que la señal de entrada disminuye su valor, no se asegura
que la frecuencia de oscilación del circuito de
relajación sea de 127 Hz.
En el diagrama de la figura 6.7 se aprecia el
ángulo de conducción a los 170º reales, que
sucedió con una valor de RE de aproximadamente
850 K.

Figura 6.7. Efecto en la carga de alterna
(170º real)
6.3.2 Carga en el lado de directa
Para simular el efecto del circuito sobre la
carga en el lado de directa, se tomó el circuito que se
muestra en la figura 6.8.
Primero se colocó RE2 de 1 ohm, para
suponer que solo estaba presente el efecto de RE1, de
tal manera que la resistencia de emisor tendría un valor
de 33 K aproximadamente. Es decir, el oscilador de
relajación estaría funcionando a su frecuencia
máxima, y por lo tanto, el SCR se tiene que disparar a
10º.
En la figura 6.9 se muestra la gráfica obtenida
en la simulación, para la señal en la carga y la
señal de disparo en la compuerta del tiristor a
10º.

Figura 6.8. Circuito con la carga en el
lado de directa

Figura 6.9. Efecto en la carga en directa
(10º)
Puede verse que el disparo ocurre aproximadamente igual
que en el caso cuando la carga estaba en el lado de alterna, pero
el voltaje en la carga es una señal de corriente
directa.
El pulso de disparo conserva sus características,
al igual que el voltaje de polarización del oscilador, por
lo que ya no se mostrarán estas
gráficas.
En la figura 6.10 está la gráfica del
disparo a 170º, cuando RE tiene un valor de 655K,
ya que como vimos anteriormente, este valor puede no ser
ideal.

Figura 6.10. Efecto en la carga en
directa (170º)

Figura 6.11. Efecto en la carga en
directa (170º real)
Puede verse en la gráfica de la figura 6.10 que,
en efecto, el disparo ocurre a los 136º, aproximadamente
igual que en el caso de la carga en alterna. De aquí, si
se hace RE igual a 850 K, se supone que el circuito se
dispara a 170º realmente, como se puede ver en la figura
6.11.
6.3.3 Frecuencia de operación del oscilador de
relajación
A partir de los datos y observaciones anteriores,
se simuló solamente el oscilador de relajación,
para obtener el rango de la frecuencia de operación. La
simulación se hizo enviando la terminal de compuerta a
tierra, para
evitar el disparo del SCR, y con la condición de la carga
en directa, como se aprecia en la figura 6.12.

Figura 6.12. Circuito para simular la
frecuencia de operación del oscilador
A partir del circuito anterior, si RE se
coloca en su valor mínimo de 33 K, se obtiene la forma de
onda de la figura 6.13, que indica una frecuencia de
oscilación de 3.59 KHz. Esto asegura que se
disparará el tiristor aproximadamente a 10º, ya que
el valor teórico inicial calculado indicaba una frecuencia
de oscilación mayor a 2160 Hz.
De igual manera, para la figura 6.14 se propuso una
RE de 850 K, que fue el valor de disparo a 170º,
obteniéndose una frecuencia de oscilación de 108
Hz, cuando la frecuencia mínima esperada
teóricamente indica 127 Hz, lo que asegura el disparo del
SCR a 170º.

Figura 6.13. Frecuencia máxima del
oscilador de relajación

Figura 6.14. Frecuencia mínima del
oscilador de relajación
PRÁCTICA
7: DISPARO LINEAL PARA EL CONTROL DE CA
7.1 Marco teórico
En las técnicas
de activación de los tiristores que se han visto hasta el
momento, la variable de control es la resistencia
eléctrica; es decir, el ángulo de disparo del
dispositivo, la tensión suministrada a la carga, y la
potencia, se controlan mediante la variación de la
resistencia de un potenciómetro.
En un sistema de control real, estos métodos
resultan tener muy pocas aplicaciones, puesto que no son tantos
los sensores que
proporcionan una variación de la resistencia ante una
cambio en la presión o
velocidad de
un motor, por
ejemplo. En cambio, es muy común que los sensores
proporcionen niveles de corriente (4 – 20 mA) y voltaje
(0.3 – 32V), puesto que es más fácil
acondicionar señales de estas características.
Aún más, los sistemas de
control digital aportan señales de control que, luego
de un conversión digital – analógica,
consisten en señales normalizadas de corriente y
tensión.
Por los motivos expuestos, los sistemas de control del
disparo de los tiristores se presentan, de una manera más
común, con una señal de referencia que es comparada
con una señal de entrada variable, en donde el tiristor (o
grupo de
ellos), es conmutada hacia conducción cuando la
señal de entrada ha sobrepasado la magnitud de la
referencia (o viceversa.)
Una forma de lograr lo antes dicho es mediante la
derivación de una señal lineal a partir de la
señal senoidal de la línea de alimentación.
Si esta señal se incrementa linealmente a partir de cero
desde el comienzo de un ciclo de la corriente alterna de entrada,
y crece a su máximo valor cuando esta señal ha
alcanzado un semiciclo (180º), entonces la magnitud de la
señal de referencia será directamente proporcional
al ángulo de variación de la señal alterna,
durante cada medio ciclo. De esta forma, una señal de
disparo basada en el monitoreo de esta señal de
referencia, podrá controlar la activación de los
tiristores en una manera linealmente proporcional al periodo de
la señal de alimentación.
7.2 Implementación del circuito de disparo
lineal
En la práctica, el circuito de disparo lineal se
compone de cuatro etapas, que se aprecian mejor en el diagrama a
bloques de la figura 7.1.
1ª etapa, Detector de cruce por cero: Esta
etapa se encarga de monitorear la señal de entrada
mediante la detección del cruce de la señal alterna
por la línea de referencia de cero, de tal forma que su
señal de salida servirá para sincronizar la
señal de alimentación y las etapas
subsecuentes.
2ª etapa, Generador de la rampa lineal:
Esta etapa consiste en un integrador que, a partir de una
tensión fija de CC, genera una rampa, cuya amplitud y
periodo se controla mediante la sincronización con la
señal de entrada.
3ª etapa, Comparador: Consiste en la
comparación de la señal producida por el integrador
y una señal de control (Ec), la cual es la señal de
salida del sistema de control (sistema digital –
análogo, señal estándar de voltaje, etc.)
Esta etapa proporcionará un nivel de tensión cuando
la rampa esté por debajo de la magnitud de la señal
de control Ec, y otro nivel cuando esté por encima de la
misma.
4ª etapa, Acoplador de señales: La
función de esta etapa es traducir los niveles de
tensión proporcionados por el comparador en una
conmutación del tiristor. En este caso, consiste en un
opto acoplador. Posteriormente a esta etapa se encuentra la etapa
de potencia, es decir el o los tiristores.
Para ver el
gráfico seleccione la opción
"Descargar"
Figura 7.1: Implementación del
circuito de disparo lineal
7.3 Material y equipo
1 TRIAC BTA08400B
1 CI TL084
3 diodos 1N4148
5 capacitores de 0.1µ 250V
1 resistencia de 15 ohms, 5 resistencias de 1k, 1
resistencia de 330, todas ½ W
1 foco de 120V 100W
2 potenciómetros de 100 k
1 MOC3011
1 transformador de aislamiento
1 transformador 120V / 3V
1 fusible 2A 250V
1 transistor 2N3904
7.4 Montaje del circuito
El circuito de la figura 7.2 ilustra acerca del montaje
real del circuito, en donde se incluyen las resistencias de
límite del opto acoplador, y el capacitor de
protección del optotriac. No se muestra el transformador
de aislamiento.

Figura 7.2: Montaje del circuito de
disparo lineal
En la práctica pudo notarse que cuando se
movía el potenciómetro R6, que está
representado un divisor de tensión variable, que
proporciona el voltaje de control, la intensidad en el foco
también se modificaba. La forma de onda vista en el
osciloscopio era muy parecida a las que se presentan en la
sección de simulación de esta
práctica.
Nótese que la variable de control no es la
resistencia del potenciómetro, como en los casos de las
prácticas anteriores, sino el voltaje que hay en el
divisor de tensión que forman sus terminales.
7.5 Simulación del circuito
Para la simulación del circuito, debido a
que las librerías de la versión 6.0 de PSPICE no
tienen los componentes necesarios, sobre todo el transformador
160V / 3V y el opto acoplador MOC3011, fue necesario modificar el
circuito, de tal forma que se ha simulado solo la parte de
disparo, omitiendo la etapa de potencia, de la que se sabe que si
le llegan los impulsos de disparo adecuados, entonces
tomará la forma de disparo discutida en la práctica
5.
La figura 7.3 muestra la parte del control lineal,
omitiendo la etapa de potencia y el opto acoplador, representando
a este por un diodo de silicio (D6). De igual forma, el
transformador de bajada de 3V se ha representado por una fuente
de voltaje controlada por voltaje, para dar una tensión de
alimentación al detector de cruce por cero de 5Vp, que
corresponde al valor pico real del transformador.
La figura 7.4 muestra las señales de entrada y de
salida del detector de cruce por cero, en donde se aprecian lo
impulsos que servirán para limitar la integración.
La figura 7.5 es la representación de PSPICE para
la señal de salida del integrador, en donde se demuestra
que el tiempo de integración está limitado por la
señal de salida del detector de cruce por cero.
En la figura 7.6 puede verse la señal de salida
del último amplificador operacional del circuito de
disparo lineal, en donde, según la posición del
opto acoplador representado por D6, existirá
conducción en el lado de potencia del opto acoplador
durante el pulso negativo del voltaje de salida del circuito de
disparo lineal.
De esta forma, se tiene que fluirá corriente de
compuerta hacia el TRIAC solo cuando el opto acoplador se active,
lo que cumple con las características de disparo del TRIAC
discutidas en la práctica 5.

Figura 7.3: Circuito usado para la
simulación del disparo lineal.

Figura 7.4: Señal de salida del
detector de cruce por cero.

Figura 7.5: Señal de salida del
integrador, el generador de rampa.

Figura 7.6: Señal de salida del
circuito de disparo lineal.
7.6 Conclusiones
El circuito de disparo lineal proporciona un alternativa
de disparo de tiristores con una mayor cantidad de aplicaciones,
puesto que es más frecuente encontrar señales de
control de voltaje o corriente, que de resistencia, como el caso
del disparo resistivo, RC o con DIAC.
EL uso de opto acoplador permite separar la etapa de
control de la etapa de potencia, reduciendo así el
riesgo de
descargas hacia los componentes más sensibles.
Se asegura que el TRIAC recibe los impulsos de disparo
adecuados al observar las señales de las figuras 7.4, 7.5
y 7.6, puesto que demuestran que los pulsos de disparo
están relacionados con la tensión de línea,
mediante el detector de cruce por cero.
Dado que el PSPICE no se encuentra un opto acoplador con
TRIAC, como el que se necesita para la práctica que se
desarrolla, la simulación de la etapa de potencia no fue
posible, pero se sabe que si el TRIAC recibe los pulsos de
disparo adecuados, entonces se comportará como un
interruptor de C.A.
PRÁCTICA
8: DISPARO LINEAL PARA UN SEMICONVERTIDOR
8.1 Marco Teórico
El circuito de disparo lineal usado para el control del
ángulo de disparo del semiconvertidor tiene la misma
configuración que la que se ha descrito en la figura 7.1.
Sin embargo, en la etapa de acoplamiento deben usarse dos opto
acopladores, cuando en el control C.A se usaba solo uno. En la
etapa de potencia no se usa un triac, sino un circuito
semiconvertidor cd –cd a
base de SCR’s.
En esta sección ya no se discutirán los
puntos referentes al diseño del circuito de control lineal
del ángulo de disparo, sino que se dedicará un poco
al estudio del comportamiento y principios del
semiconvertidor.
8.1.1 Introducción a los
semiconvertidores
Los circuitos rectificadores con diodos proporcionan un
voltaje de corriente directa fijo. Para obtener voltajes de
salida controlados, se utilizan tiristores. Es posible modificar
la magnitud del voltaje de salida de los rectificadores a
tiristores controlando el ángulo de disparo de los mismos.
Un tiristor funcionando en esta forma se conoce como tiristor de
control de fase, que se activa mediante la aplicación de
un disparo en la compuerta y se desactiva mediante la
conmutación natural o de línea.
Los rectificadores controlados por fase son sencillos,
económicos y logran eficiencias del orden de 95%. Se
conocen como convertidores de ca – cd, puesto que
transforman el valor de una tensión alterna en una
tensión directa.
Para evaluar el funcionamiento y el rendimiento de un
convertidor se utilizan las series de Fourier, en donde se supone
que la inductancia de la carga es lo suficientemente alta para
que la corriente de la carga se considere continua y tenga una
componente ondulatoria despreciable. En el presente reporte se
evaluará solo el caso de un semiconvertidor de onda
completa, cuyo diagrama esquemático se muestra en la
figura 8.1.

Figura 8.1: Diagrama general del
semiconvertidor.
8.1.2 Desarrollo matemático de las expresiones
en los semiconvertidores
Según el diagrama de la figura 8.1, se
analizará el circuito para obtener sus principales
parámetros, considerando que el tiristor T1 se dispara
en w
t=a , y el
tiristor T2 en w
t= a
+ p , de
tal forma que se considerarán los siguientes valores para
los ángulos:
a | a | a | a |
a | p | a | 2p |
De esta manera, se evaluarán los siguientes
datos, para valores de a de 10, 90 y 170 grados
eléctricos.
![]()
![]()

 ,
, ![]()
![]() ,
, ![]()
![]() ,
, 
A partir de las expresiones anteriores, se llenó
la tabla siguiente, para los distintos valores del ángulo
de disparo dados previamente, para Vm=170V.
a | THDI | FP | VCD | VRMS |
10 deg | 41.72 % | 0.9194 | 107.4 | |
90 deg | 48.35 % | 0.6366 | 54.113 | |
170 deg | 283.3 % | 0.0290 | 0.8221 |
Tabla 8.1: Valores teóricos de los
parámetros del semiconvertidor.
8.1.3 Simulación de un semiconvertidor con
pulsos de disparo ideales
Para comparar los valores obtenidos mediante las
expresiones matemáticas teóricas, y que se
recopilan en la tabla 8.1, con los valores reales que se tienen
en un circuito en donde no se pueden considerar como
despreciables muchos de los valores que se consideran para el
análisis matemático (inductancia
infinita, corriente directa, armónicas adicionales), se
recurrió a una simulación en PSPICE.
El circuito usado para la simulación se muestra
en la figura 8.2, en donde los pulsos de disparo se generan
mediante fuentes de pulso periódicas, y la fuente de
alimentación tiene un valor pico de 170 V de corriente
alterna de 60 Hz.
Las resistencias R1 y R2 tienen este valor para limitar
la corriente de compuerta a 47 mA, puesto que el SCR usado tiene
una IGT de 40 mA. También por este motivo la
magnitud de las fuentes de disparo es de 5V. El ancho de pulso de
disparo es de 20µs, en tanto el SCR tiene un tiempo de
encendido del tiristor es de 1µs, por lo que es un tiempo
suficiente para hacerlo conmutar.
El diodo de marcha libre se ha colocado como una
indicación de que, para cargas altamente inductivas, este
diodo es recomendable.
La resistencia de carga RL se ha sugerido de este valor
en forma arbitraria y la inductancia L1 ha sido colocada de un
valor suficientemente grande para considerar la corriente como
directa, y suficientemente pequeño para no provocar
errores de convergencia. (Como nota adicional se cometa que fue
necesario cambiar los valores RELTOL, VNTOL y ABSTOL en el
simulador.)
Para el análisis de las frecuencias
armónicas se ha colocado una resistencia adicional Rs, de
valor muy pequeño, de tal manera que la variable de
análisis fuera la corriente por esta resistencia,
considerando una frecuencia fundamental de 60 Hz, y 31
armónicas secundarias.

Figura 8.2: Circuito usado para la
simulación en PSPICE
8.1.3.1. Simulación para
a =10
grados
Para este ángulo de disparo, el tiristor T1 debe
de encenderse a un ángulo de 10 grados, correspondiente a
462.97µs, en tanto T2, que debe conmutar a 190 grados o
8.7965µs. Lo anterior se tomó en cuenta a cuando se
asignaron valores a las fuentes de disparo.
En la figura 8.3 se dibuja una gráfica obtenida
en la simulación para el ángulo de disparo dado. Se
puede notar que los SCR están activándose
aproximadamente a los 10 grados de su respectivo semiciclo de
operación.

Figura 8.3: Forma de onda en RL
para a =10
grados
Para obtener la gráfica anterior solo se
simuló una pequeña porción de tiempo. En la
figura 8.4 aparece el valor promedio para el voltaje de salida de
este circuito, teniendo que haber evaluado este durante un tiempo
mayor, como puede apreciarse en la misma
gráfica.
Como puede notarse, el valor promedio de la
simulación es de aproximadamente 102.5 VCD, que coincide
aproximadamente con el voltaje esperado teóricamente de
107 VCD. Es necesario decir que para obtener este valor fue
necesario simular durante unos 400ms para que se estabilizara el
valor promedio, donde fueron necesarios unos 24 ciclos de la
señal de entrada.
En adición, se debe mencionar que para que la
simulación no presentara problemas de convergencia, el
valor de la inductancia fue ajustado a 15mH solamente, ya que si
se sobrepasaba este valor, el simulador marcaba errores de
aproximación numérica.

Figura 8.4: Voltaje promedio del voltaje
de salida, 10 grados
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |






